在数学的广阔领域中,概率运算占据着举足轻重的地位。它不仅是统计学、机器学习、数据分析等现代科学技术的基础,也深刻地影响着我们的日常生活决策。当我们谈论“概率运算的五个基本公式”时,实际上是在探讨一系列核心原理,这些原理为我们提供了理解和计算随机事件可能性的有力工具。以下是围绕这一主题展开的详细探讨。
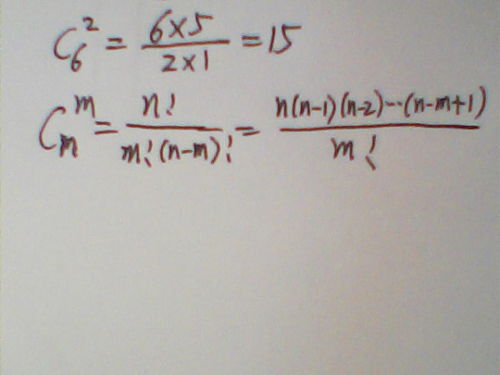
概率运算的基础建立在两个核心概念之上:随机事件和概率。随机事件是指在一定条件下,并不总是发生,也不总是不发生的现象;而概率则是用来量化这种事件发生可能性的数值,通常表示为介于0和1之间的一个实数,其中0表示不可能事件,1表示必然事件。
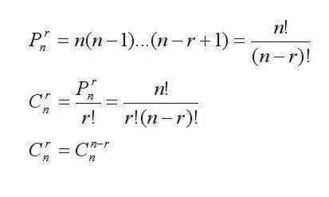
1. 加法公式(和公式)
概率的加法公式,也被称为和公式或并集公式,它描述了两个或多个事件至少有一个发生的概率如何计算。具体来说,如果事件A和事件B是两个互斥(即不能同时发生)的事件,那么它们至少有一个发生的概率P(A∪B)等于各自发生的概率之和,即P(A∪B) = P(A) + P(B)。然而,如果事件A和B不是互斥的,则需要从两者之和中减去它们同时发生的概率以避免重复计算,公式变为P(A∪B) = P(A) + P(B) - P(A∩B)。这一公式在处理多个可能同时发生的随机事件时尤为有用,比如在计算某个复合疾病的发生率时,就需要考虑各个致病因素单独及共同作用的可能性。
2. 乘法公式(条件概率公式)
概率的乘法公式,或称条件概率公式,是处理条件概率问题的基础。条件概率是指在某个特定事件已经发生的条件下,另一个事件发生的概率。它的一般形式是P(A|B) = P(A∩B) / P(B),其中P(A|B)表示在B发生的条件下A发生的概率,P(A∩B)是A和B同时发生的概率,P(B)是B发生的概率。这个公式的重要性在于它建立了两个事件之间的依赖关系,使得我们可以在已知一个事件发生的情况下,更新对另一个事件发生概率的估计。在实际应用中,条件概率公式广泛用于贝叶斯定理、马尔可夫链等高级概率模型中。

3. 全概率公式
全概率公式是一个非常重要的工具,用于计算复杂随机事件发生的概率,特别是当这个事件可以由多个互斥且完备的原因引起时。完备性意味着这些原因覆盖了所有可能的情况,互斥性则意味着这些原因不能同时发生。全概率公式表达为P(A) = Σ P(Bi)P(A|Bi),其中Bi是引起事件A的互斥且完备的原因,P(Bi)是原因Bi发生的概率,P(A|Bi)是在原因Bi发生的条件下事件A发生的概率。这个公式在故障诊断、决策分析等领域有着广泛的应用,它允许我们从多个可能的原因出发,综合评估一个事件发生的总概率。
4. 贝叶斯定理
贝叶斯定理是概率论中一个极其重要的结果,它提供了一种根据新的信息更新信念或概率的方法。其基本形式为P(Bi|A) = [P(Bi)P(A|Bi)] / Σ [P(Bj)P(A|Bj)],其中P(Bi|A)是在观察到事件A后,原因Bi成立的概率(后验概率),P(Bi)是原因Bi的先验概率(即在没有任何额外信息的情况下的概率),P(A|Bi)是在原因Bi成立的条件下事件A发生的概率(似然度),Σ表示对所有可能原因Bj的求和。贝叶斯定理在医疗诊断、垃圾邮件过滤、自然语言处理等领域发挥着关键作用,它让我们能够根据新的证据动态调整我们的信念。
5. 独立性公式
独立性是概率论中的一个基本概念,它描述了两个或多个事件之间是否存在相互影响。如果事件A的发生不影响事件B的发生概率,即P(A∩B) = P(A)P(B),则称事件A和B是相互独立的。独立性公式不仅是一个定义,它还在许多实际应用中起到了简化计算的作用。例如,在抛掷一枚公平的六面骰子时,每一面出现的概率是独立的,不受之前或之后投掷结果的影响。理解并应用独立性公式,可以帮助我们更准确地评估复杂系统中各个组成部分之间的相互作用。
综上所述,概率运算的五个基本公式构成了理解和处理随机现象的强大框架。加法公式和乘法公式提供了计算单个和复合事件发生概率的基本方法;全概率公式和贝叶斯定理则进一步扩展了我们的能力,使我们能够在更复杂的情境中评估概率;而独立性公式则揭示了事件之间是否存在相互影响,为简化概率计算提供了依据。这些公式不仅在数学理论上具有深远的意义,更在解决实际问题时展现出了惊人的实用性。无论是科学研究、工程设计还是日常决策,深入理解并灵活应用




























相关文章