圆柱的侧面积,这一几何概念,对于许多初学者或是需要重温基础数学知识的人来说,或许是个既熟悉又略显陌生的话题。在深入探究之前,让我们先明确一点:圆柱,作为一种基本的立体几何形状,其特性由两个平行的圆形底面以及连接这两个底面的侧面所构成。而侧面积,正是这个侧面展开后所形成的平面图形的面积。
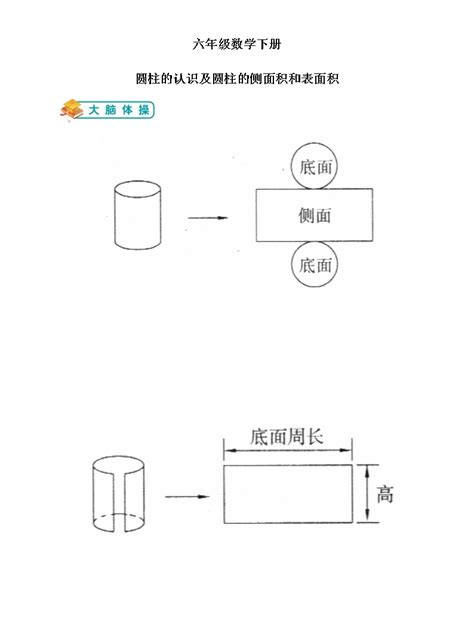
要了解圆柱的侧面积如何计算,我们首先要认识到,圆柱的侧面如果沿高展开,将会形成一个矩形。这个矩形的长,等于圆柱的底面周长;而矩形的宽,则恰好是圆柱的高。因此,计算圆柱侧面积的公式,便源自这一几何变换的逻辑。
具体地说,圆柱的底面周长C,可以通过圆的周长公式C=2πr得出,其中r代表圆柱底面的半径。有了这个基础,圆柱的侧面积S便可以通过矩形的面积公式来计算,即长乘以宽,也就是底面周长乘以高,用数学表达式表示为S=Ch,或者将C的公式代入,得到S=2πrh。
这个公式是圆柱侧面积计算的核心,它简洁而直观,揭示了圆柱侧面积与底面半径和高之间的数量关系。对于任何给定的圆柱,只要我们知道了它的底面半径和高,就可以轻松计算出它的侧面积。
然而,理解这个公式并不仅仅是数学上的运算,更是一种几何直觉的培养。想象一下,你手持一个圆柱形的纸筒,沿着它的高将其侧面剪开,一个矩形便跃然眼前。这个矩形的长度,恰好等于圆柱底面的周长,而宽度,则是圆柱的高度。这种从三维到二维的转换,不仅让我们得以用更简单的二维图形来计算原本复杂的三维面积,也加深了我们对于空间几何形状的理解。
在实际应用中,圆柱的侧面积计算有着广泛的应用。比如,在制作圆柱形包装材料时,设计师需要准确计算出侧面积,以确保包装材料的尺寸恰到好处,既能紧密贴合圆柱体,又不会浪费材料。在建筑工程中,圆柱形的柱子或管道的表面处理,同样需要精确计算侧面积,以便合理估算涂料或装饰材料的用量。
此外,圆柱的侧面积还与一些物理现象密切相关。例如,在流体动力学中,圆柱体的侧面积会影响其在流体中的阻力特性。一个表面积较大的圆柱体,在流体中运动时,会受到更大的阻力,这在设计水下航行器或飞行器时尤为重要。
当然,圆柱的侧面积只是圆柱几何特性的一部分。圆柱的体积、表面积(包括侧面积和底面积)等都是重要的几何量,它们共同构成了圆柱这一几何形状的完整描述。但在许多实际应用场景中,侧面积往往是关注的焦点,因为它直接关系到材料的消耗、处理难度以及物理性能等方面。
值得一提的是,圆柱的侧面积公式不仅适用于正圆柱(即底面为圆形的直圆柱),在一些特殊情况下,也可以通过类比或变换的方法,应用于其他类型的圆柱体。比如,对于底面为椭圆形的椭圆圆柱,虽然其侧面积的计算公式会更为复杂,但基本原理仍然是基于侧面展开后的图形面积来计算。
总之,圆柱的侧面积等于底面周长乘以高,这一公式简洁而强大,它不仅是数学计算的基础,更是连接理论与实践的桥梁。通过深入理解这一公式,我们可以更好地把握圆柱这一几何形状的本质特性,进而在实际应用中做出更加准确和高效的决策。
对于那些对圆柱侧面积感兴趣的朋友来说,掌握这一公式只是起点。随着学习的深入,你会发现,几何学的世界远比这更复杂、更精彩。圆柱只是众多几何形状中的一种,而侧面积的计算也只是几何学众多应用中的一个方面。但正是这些看似简单却充满智慧的知识点,构成了我们理解和改造世界的基石。希望这篇文章能够激发你对几何学的兴趣,引领你走进这个充满奥秘与美的世界。


























相关文章